Population Coding in Spiking Neural Nets

Tutorial written by Jason K. Eshraghian (www.jasoneshraghian.com)

Open In Colab

The snnTorch tutorial series is based on the following paper. If you find these resources or code useful in your work, please consider citing the following source:

Note

This tutorial is a static non-editable version. Interactive, editable versions are available via the following links:

Introduction

It is thought that rate codes alone cannot be the dominant encoding mechanism in the primary cortex. One of several reasons is because the average neuronal firing rate is roughly \(0.1-1\) Hz, which is far slower than the reaction response time of animals and humans.

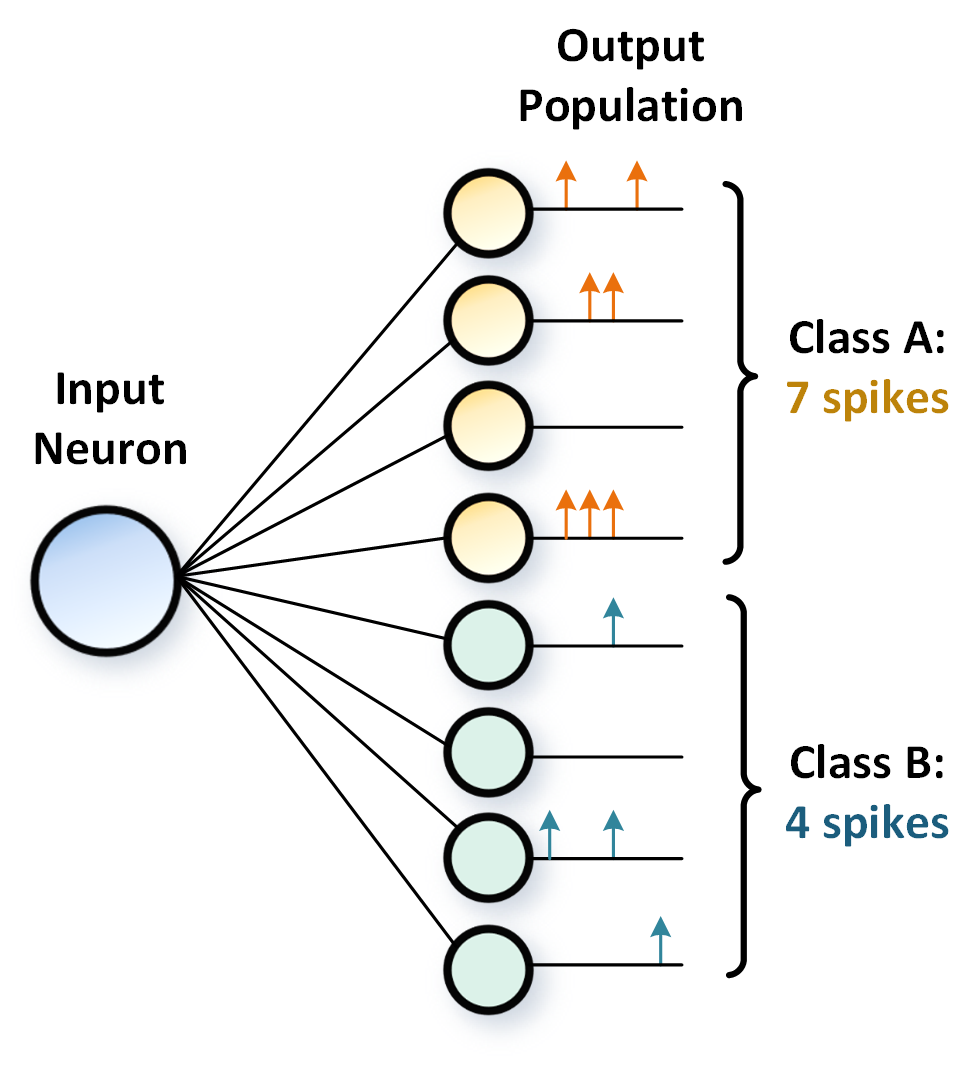
But if we pool together multiple neurons and count their spikes together, then it becomes possible to measure a firing rate for a population of neurons in a very short window of time. Population coding adds some credibility to the plausibility of rate-encoding mechanisms.

https://github.com/jeshraghian/snntorch/blob/master/docs/_static/img/examples/tutorial_pop/pop.png?raw=true

In this tutorial, you will:

  • Learn how to train a population coded network. Instead of assigning one neuron per class, we will extend this to multiple neurons per class, and aggregate their spikes together.

!pip install snntorch

import torch, torch.nn as nn
import snntorch as snn

DataLoading

Define variables for dataloading.

batch_size = 128
data_path='/tmp/data/fmnist'
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("mps") if torch.backends.mps.is_available() else torch.device("cpu")

Load FashionMNIST dataset.

from torch.utils.data import DataLoader
from torchvision import datasets, transforms

# Define a transform
transform = transforms.Compose([
            transforms.Resize((28, 28)),
            transforms.Grayscale(),
            transforms.ToTensor(),
            transforms.Normalize((0,), (1,))])

fmnist_train = datasets.FashionMNIST(data_path, train=True, download=True, transform=transform)
fmnist_test = datasets.FashionMNIST(data_path, train=False, download=True, transform=transform)

# Create DataLoaders
train_loader = DataLoader(fmnist_train, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(fmnist_test, batch_size=batch_size, shuffle=True)

Define Network

Let’s compare the performance of a pair of networks both with and without population coding, and train them for one single time step.

from snntorch import surrogate

# network parameters
num_inputs = 28*28
num_hidden = 128
num_outputs = 10
num_steps = 1

# spiking neuron parameters
beta = 0.9  # neuron decay rate
grad = surrogate.fast_sigmoid()

Without population coding

Let’s just use a simple 2-layer dense spiking network.

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(num_inputs, num_hidden),
                    snn.Leaky(beta=beta, spike_grad=grad, init_hidden=True),
                    nn.Linear(num_hidden, num_outputs),
                    snn.Leaky(beta=beta, spike_grad=grad, init_hidden=True, output=True)
                    ).to(device)

With population coding

Instead of 10 output neurons corresponding to 10 output classes, we will use 500 output neurons. This means each output class has 50 neurons randomly assigned to it.

pop_outputs = 500

net_pop = nn.Sequential(nn.Flatten(),
                        nn.Linear(num_inputs, num_hidden),
                        snn.Leaky(beta=beta, spike_grad=grad, init_hidden=True),
                        nn.Linear(num_hidden, pop_outputs),
                        snn.Leaky(beta=beta, spike_grad=grad, init_hidden=True, output=True)
                        ).to(device)

Training

Without population coding

Define the optimizer and loss function. Here, we use the MSE Count Loss, which counts up the total number of output spikes at the end of the simulation run.

The correct class has a target firing probability of 100%, and incorrect classes are set to 0%.

import snntorch.functional as SF

optimizer = torch.optim.Adam(net.parameters(), lr=2e-3, betas=(0.9, 0.999))
loss_fn = SF.mse_count_loss(correct_rate=1.0, incorrect_rate=0.0)

We will also define a simple test accuracy function that predicts the correct class based on the neuron with the highest spike count.

from snntorch import utils

def test_accuracy(data_loader, net, num_steps, population_code=False, num_classes=False):
  with torch.no_grad():
    total = 0
    acc = 0
    net.eval()

    data_loader = iter(data_loader)
    for data, targets in data_loader:
      data = data.to(device)
      targets = targets.to(device)
      utils.reset(net)
      spk_rec, _ = net(data)

      if population_code:
        acc += SF.accuracy_rate(spk_rec.unsqueeze(0), targets, population_code=True, num_classes=10) * spk_rec.size(1)
      else:
        acc += SF.accuracy_rate(spk_rec.unsqueeze(0), targets) * spk_rec.size(1)

      total += spk_rec.size(1)

  return acc/total

Let’s run the training loop. Note that we are only training for \(1\) time step. I.e., each neuron only has the opportunity to fire once. As a result, we might not expect the network to perform too well here.

from snntorch import backprop

num_epochs = 5

# training loop
for epoch in range(num_epochs):

    avg_loss = backprop.BPTT(net, train_loader, num_steps=num_steps,
                          optimizer=optimizer, criterion=loss_fn, time_var=False, device=device)

    print(f"Epoch: {epoch}")
    print(f"Test set accuracy: {test_accuracy(test_loader, net, num_steps)*100:.3f}%\n")

    >> Epoch: 0
    >> Test set accuracy: 59.421%

    >> Epoch: 1
    >> Test set accuracy: 61.889%

While there are ways to improve single time-step performance, e.g., by applying the loss to the membrane potential, one single time-step is extremely challenging to train a network competitively using rate codes.

With population coding

Let’s modify the loss function to specify that population coding should be enabled. We must also specify the number of classes. This means that there will be a total of \(50~neurons~per~class~=~500~neurons~/~10~classes\).

loss_fn = SF.mse_count_loss(correct_rate=1.0, incorrect_rate=0.0, population_code=True, num_classes=10)
optimizer = torch.optim.Adam(net_pop.parameters(), lr=2e-3, betas=(0.9, 0.999))

num_epochs = 5

# training loop
for epoch in range(num_epochs):

    avg_loss = backprop.BPTT(net_pop, train_loader, num_steps=num_steps,
                            optimizer=optimizer, criterion=loss_fn, time_var=False, device=device)

    print(f"Epoch: {epoch}")
    print(f"Test set accuracy: {test_accuracy(test_loader, net_pop, num_steps, population_code=True, num_classes=10)*100:.3f}%\n")

    >> Epoch: 0
    >> Test set accuracy: 80.501%

    >> Epoch: 1
    >> Test set accuracy: 82.690%

Even though we are only training on one time-step, introducing additional output neurons has immediately enabled better performance.

Conclusion

The performance boost from population coding may start to fade as the number of time steps increases. But it may also be preferable to increasing time steps as PyTorch is optimized for handling matrix-vector products, rather than sequential, step-by-step operations over time.